GMES는 맥스웰 방정식을 수치해석적으로 푸는 FDTD라는 방법을 구현한 프로그램이다. 맥스웰 방정식을 푼다는 점은 전자기 현상을 다룬다는 의미와 이를 양자역학적 해석보다는 고전역학적 해석으로 다룬다는 의미가 있다. FDTD는 우리가 생활하는 공간과 같은 시공간을 그대로 사용하는 방식으로 주파수 공간이나 파수 공간을 사용하는 방식과는 달리, 실제 실험과 유사한 방식으로 계산 공간을 설정할 수 있는 장점이 있다. 즉, 실험 모형과 입력 광원 등을 모두 머릿속에 쉽게 그려볼 수 있다.
GMES의 검증도 겸할까 해서, 학부 물리학과 2학년에 전자기학에서 배우는 쉬운 실험 모형을 하나 골랐다. 바로 두 유전체의 경계면에 입사하는 평면파 모형이다. 이중에서 입력 광원에 대해 살펴보자. 먼저, 이 모의실험에 사용할, 제대로 된 평면파의 모습은 아래와 같다.
 |
| 정상적인 평면파의 모습 |
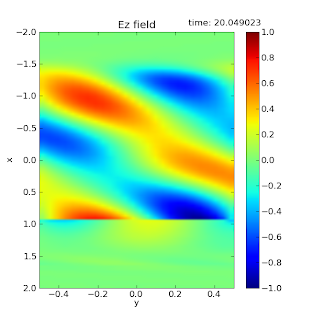 |
| 허수부 위상을 맞추지 못해 변형된 평면파 |
첫 그림의 왼쪽과 오른쪽 끝을 비교해보자. 오른쪽 경계에 다다른 전자기파는 다시 왼쪽 경계로 다시 입력된다고 했는데, 뭔가 이상하지 않은가? 왼쪽과 오른쪽의 경계를 맞춰보면 일치하지 않고 약간 틀어져 있는 것을 알 수 있다. 즉, 어느 정도의 위상차가 있다. 평면파의 위상을 맞추려면, 오른쪽 끝의 전자기파와 왼쪽 끝의 전자기파에 일정 위상차를 주어야 하는데, 이런 위상차를 주려면 전자기파를 복소수로 나타내야 한다. 복소수로 나타낸 전자기파는 단순한 곱셈으로 진폭의 변화 없이 일정 위상만큼 변화를 줄 수 있다.
그럼, 위에서 열거한 것 중에서 뭐가 문제일까? 개별 요소들은 각기 다른 환경에서 검증을 진행해 온 상태이다. 아직 검증하지 못한 부분에 버그가 존재할 수도 있고, 이들의 조합에서 문제가 발생할 수도 있다. 아니면, 내가 뭔가 잘 못 생각하고 있을 수도 있다. 내가 뭘 놓치고 있을까? 모든 가능성을 염두에 두고 print를 이용한 디버깅 정보 수집에 나섰다. 그러던 중 우연히 프로그램 일부가 실수 전자기파를 사용하고 있음을 알 수 있었다. 그리고 그 부분을 찾아보니 입력 광원 구현부였다. 입력 평면을 따라 전자기파의 실수부는 계속 변하는데, 허수부는 일정 위상(0)을 유지하고 있으니, 당연히 문제가 되었던 것이다. 이를 수정하니, 첫 번째 그림과 같은 정상적인 평면파를 볼 수 있었다.






